Regression
Chapter 5.0 - 5.1

Today’s goals


  1. Find the correlation between two variables
  2. Build and interpret a linear regression model
  3. Make predictions using a linear regression model
  4. Plot the line of best fit on a scatterplot

Artwork by @allison_horst

A Note about Regression


Remember that, BEFORE building a model, you should conduct an exploratory data analysis.


You will almost certainly need to do some data wrangling and visualizations before the model analysis.


For this lessons example we will be using a subset of the penguins dataset that only includes male penguins from the Chinstrap species and Dream island. This is stored in penguin_sub.

Correlation Coefficient (Ex1)

Correlation coefficient: a number between -1 and 1 indicating the strength of the linear relationship between two numerical variables.

The correlation coefficient (\(r\)) between a variable with values \(x_1,...,x_n\), and a variable with values \(y_1,...,y_n\) is defined as:

\(Correlation(r) = \frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^n(x_i-\bar{x})^2\sum_{i=1}^n(y_i-\bar{y})^2}},\)

where \(\bar{x}\) is the mean of \(x_1,...,x_n\), and \(\bar{y}\) is the mean of \(y_1,...,y_n\)

Is correlation between two variables \(X\) and \(Y\) the same as the correlation between \(Y\) and \(X\)?

Correlation Coefficient (Ex1)

Match the following graphs with the most appropriate correlation coefficient:

  1.     a) -0.2     b) 0     c) 0.4     d) 0.7

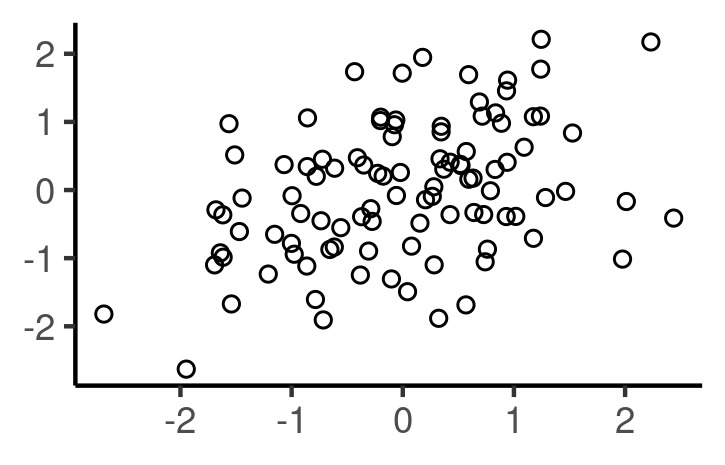
Correlation Coefficient (Ex2)

Match the following graph with the most appropriate correlation coefficient:

  1.     a) -1     b) -0.75     c) -0.9     d) 1

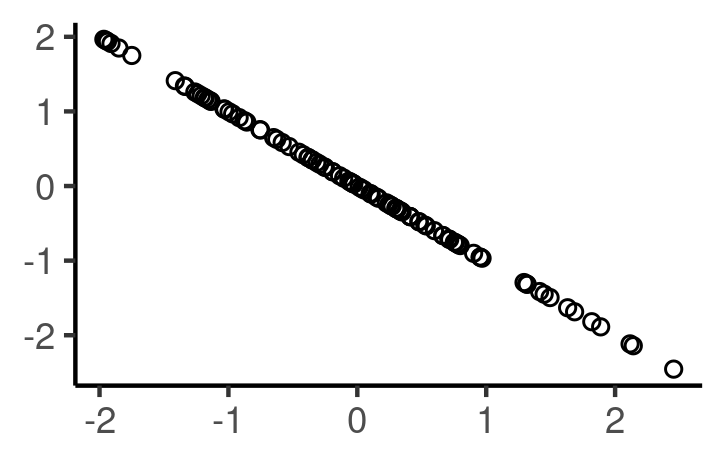
Correlation Coefficient (Ex3)

Match the following graph with the most appropriate correlation coefficient:

  1. Amount of gas in a car vs distance traveled .

    a . Exactly -1

    b . Between -1 and 0

    c . About 0

    d . Between 0 and 1

    e . Exactly 1

Correlation does not imply causation, as is evident from this example.

Correlation Coefficient (continued)

The following code shows three different options for calculating the correlation between two variables within the penguins dataset. 

# Option 1
penguin_sub %>%
  select(flipper_length_mm, body_mass_g) %>% 
  cor()
# Option 2
penguin_sub %>%
    summarize(cor = cor(flipper_length_mm, body_mass_g) )
# Option 3
cor(penguins$flipper_length_mm, penguins$body_mass_g)
penguin_sub <- penguins %>% 
  filter(sex == "male", species == "Chinstrap", island == "Dream") %>% 
  mutate(id = seq(1:34))

glimpse(penguin_sub)
Rows: 34
Columns: 9
$ species           <fct> Chinstrap, Chinstrap, Chinstrap, Chinstrap, Chinstra…
$ island            <fct> Dream, Dream, Dream, Dream, Dream, Dream, Dream, Dre…
$ bill_length_mm    <dbl> 50.0, 51.3, 52.7, 51.3, 51.3, 51.7, 52.0, 50.5, 50.3…
$ bill_depth_mm     <dbl> 19.5, 19.2, 19.8, 18.2, 19.9, 20.3, 18.1, 19.6, 20.0…
$ flipper_length_mm <int> 196, 193, 197, 197, 198, 194, 201, 201, 197, 195, 19…
$ body_mass_g       <int> 3900, 3650, 3725, 3750, 3700, 3775, 4050, 4050, 3300…
$ sex               <fct> male, male, male, male, male, male, male, male, male…
$ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…
$ id                <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1…

You will most likely need to filter out missing data beforehand OR set use = "complete.obs" inside the cor() function. This is the equivalent of when we set na.rm = TRUE in other summary functions.

Simple Linear Regression (SLR)

  • Definition: Simple linear regression: models the relationship between a response (y) variable and one explanatory (x) variable.
  • Essentially, we are finding the line of best fit for a scatterplot between ‘x’ and ‘y’.

SLR (continued)

Equation of a regression line: \[\hat{y} = b_0 + b_1*x\]


  • \(b_0\) : intercept; the expected value of \(\hat{y}\) when \(x = 0\)

  • \(b_1\) : slope; for every 1 unit increase in x, then \(\hat{y}\) increases on average by \(b_1\)

  • fitted values: \(\hat{y}\); the predicted value on the regression line

  • residuals: \(y - \hat{y}\); error in prediction

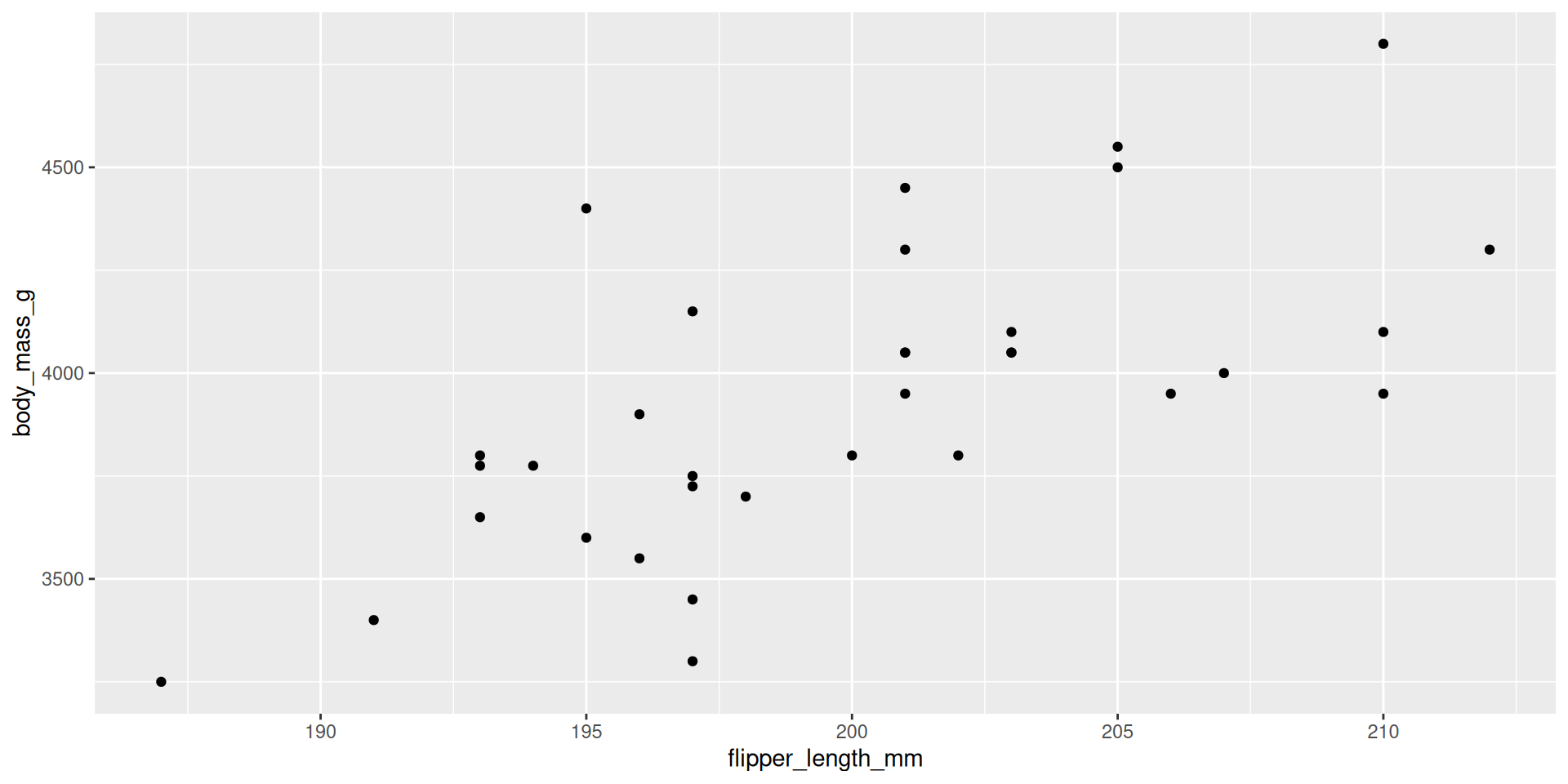
Example 1: Model

Consider a subset of the penguins dataset that only includes male penguins from the Chinstrap species and Dream island. This is stored in penguin_sub.

Predict a penguin’s body_mass_g using flipper_length_mm.

#Build a model
model_penguin <- lm(body_mass_g ~ flipper_length_mm, data = penguin_sub)
penguin_sub <- penguins %>% 
  filter(sex == "male", species == "Chinstrap", island == "Dream")%>% 
  mutate(id = seq(1:34))

glimpse(penguin_sub)
Rows: 34
Columns: 9
$ species           <fct> Chinstrap, Chinstrap, Chinstrap, Chinstrap, Chinstra…
$ island            <fct> Dream, Dream, Dream, Dream, Dream, Dream, Dream, Dre…
$ bill_length_mm    <dbl> 50.0, 51.3, 52.7, 51.3, 51.3, 51.7, 52.0, 50.5, 50.3…
$ bill_depth_mm     <dbl> 19.5, 19.2, 19.8, 18.2, 19.9, 20.3, 18.1, 19.6, 20.0…
$ flipper_length_mm <int> 196, 193, 197, 197, 198, 194, 201, 201, 197, 195, 19…
$ body_mass_g       <int> 3900, 3650, 3725, 3750, 3700, 3775, 4050, 4050, 3300…
$ sex               <fct> male, male, male, male, male, male, male, male, male…
$ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…
$ id                <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1…

Example 1: Model

Consider a subset of the penguins dataset that only includes male penguins from the Chinstrap species and Dream island. This is stored in penguin_sub.

Predict a penguin’s body_mass_g using flipper_length_mm.

#Build a model

model_penguin <- lm(body_mass_g ~ flipper_length_mm, data = penguin_sub)

#Summarize the model
summary(model_penguin)

Call:
lm(formula = body_mass_g ~ flipper_length_mm, data = penguin_sub)

Residuals:
    Min      1Q  Median      3Q     Max 
-521.72 -177.33  -23.06  117.51  658.82 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)       -4111.348   1600.726  -2.568   0.0151 *  
flipper_length_mm    40.269      8.004   5.031 1.81e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 274.8 on 32 degrees of freedom
Multiple R-squared:  0.4417,    Adjusted R-squared:  0.4242 
F-statistic: 25.31 on 1 and 32 DF,  p-value: 1.814e-05
penguin_sub <- penguins %>% 
  filter(sex == "male", species == "Chinstrap", island == "Dream") %>% 
  mutate(id = seq(1:34))

glimpse(penguin_sub)
Rows: 34
Columns: 9
$ species           <fct> Chinstrap, Chinstrap, Chinstrap, Chinstrap, Chinstra…
$ island            <fct> Dream, Dream, Dream, Dream, Dream, Dream, Dream, Dre…
$ bill_length_mm    <dbl> 50.0, 51.3, 52.7, 51.3, 51.3, 51.7, 52.0, 50.5, 50.3…
$ bill_depth_mm     <dbl> 19.5, 19.2, 19.8, 18.2, 19.9, 20.3, 18.1, 19.6, 20.0…
$ flipper_length_mm <int> 196, 193, 197, 197, 198, 194, 201, 201, 197, 195, 19…
$ body_mass_g       <int> 3900, 3650, 3725, 3750, 3700, 3775, 4050, 4050, 3300…
$ sex               <fct> male, male, male, male, male, male, male, male, male…
$ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…
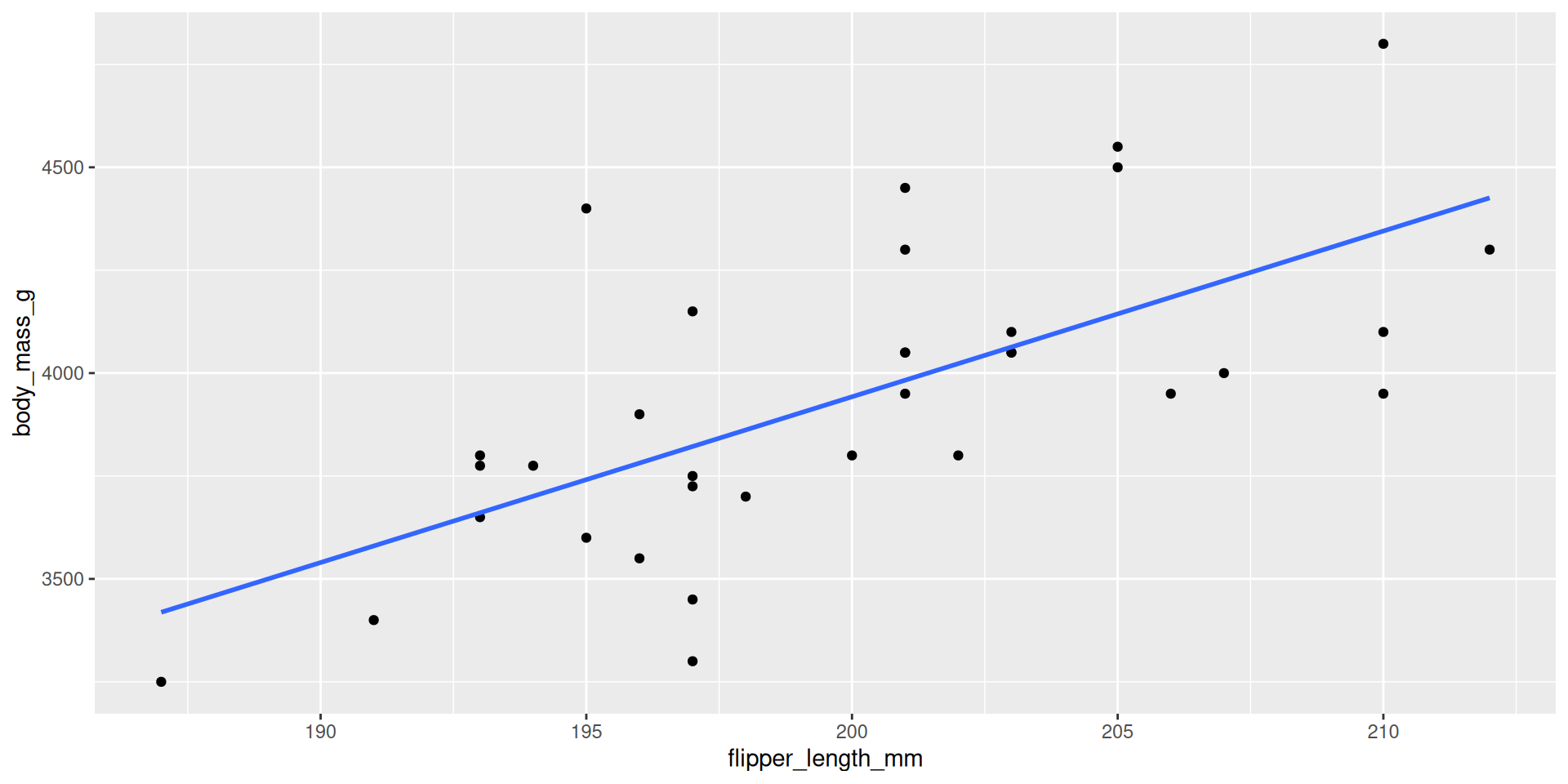
$ id                <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1…

Example 1: Plot regression line

# Plot relationship of variables
ggplot(penguin_sub, aes(x = flipper_length_mm, y = body_mass_g))+
    geom_point()

summary(model_penguin)$coefficients
                     Estimate  Std. Error   t value     Pr(>|t|)
(Intercept)       -4111.34753 1600.725516 -2.568428 1.508617e-02
flipper_length_mm    40.26936    8.003689  5.031349 1.814086e-05

Example 1: Plot regression line

# Add line of best fit
ggplot(penguin_sub, aes(x = flipper_length_mm, y = body_mass_g))+
    geom_point() +
  geom_smooth(method = "lm", se = FALSE)

summary(model_penguin)$coefficients
                     Estimate  Std. Error   t value     Pr(>|t|)
(Intercept)       -4111.34753 1600.725516 -2.568428 1.508617e-02
flipper_length_mm    40.26936    8.003689  5.031349 1.814086e-05

Example 1: Residuals

Predict a penguin’s body_mass_g using flipper_length_mm.

penguin_sub <- penguin_sub %>% 
  mutate(fitted = fitted(model_penguin),
         residuals = residuals(model_penguin))

glimpse(penguin_sub)
Rows: 34
Columns: 11
$ species           <fct> Chinstrap, Chinstrap, Chinstrap, Chinstrap, Chinstra…
$ island            <fct> Dream, Dream, Dream, Dream, Dream, Dream, Dream, Dre…
$ bill_length_mm    <dbl> 50.0, 51.3, 52.7, 51.3, 51.3, 51.7, 52.0, 50.5, 50.3…
$ bill_depth_mm     <dbl> 19.5, 19.2, 19.8, 18.2, 19.9, 20.3, 18.1, 19.6, 20.0…
$ flipper_length_mm <int> 196, 193, 197, 197, 198, 194, 201, 201, 197, 195, 19…
$ body_mass_g       <int> 3900, 3650, 3725, 3750, 3700, 3775, 4050, 4050, 3300…
$ sex               <fct> male, male, male, male, male, male, male, male, male…
$ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…
$ id                <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1…
$ fitted            <dbl> 3781.446, 3660.638, 3821.716, 3821.716, 3861.985, 37…
$ residuals         <dbl> 118.55366, -10.63827, -96.71570, -71.71570, -161.985…

Example 1: Predicting

Recall the equation of the regression line is

\[\widehat{\hbox{body_mass_g} } = -4111.3 + 40.3*\hbox{flipper_length}\]


You find a new male penguin from the Chinstrap species and Dream island that has a flipper length of 220 mm. What do you predict his weight to be in grams?

```{r}
-4111.3 + 40.3*220
```
[1] 4754.7